From the Editor
 How
do you interpret serological tests from a farm? How sure are you
of the decisions you make with those test results? Epidemiologists
use the terms sensitivity, specificity, positive predictive value,
and negative predictive value to attach a probability to the correctness
of the test results. Although this is not a precise science, and
therefore the numbers are not exact, it does give us an opportunity
to put some balance in our interpretations.
How
do you interpret serological tests from a farm? How sure are you
of the decisions you make with those test results? Epidemiologists
use the terms sensitivity, specificity, positive predictive value,
and negative predictive value to attach a probability to the correctness
of the test results. Although this is not a precise science, and
therefore the numbers are not exact, it does give us an opportunity
to put some balance in our interpretations.
Let's use the IDEXX ELISA test for the PRRS virus as a working example to help us understand these epidemiological terms. The sensitivity of the test is the ability of the test to correctly identify all truly positive (exposed) animals. For this discussion "true positives" will be animals that were exposed to the field virus at least 14 days prior to testing. Assuming that we wait 14 days after exposure before testing, the sensitivity of the test is expected to be high, perhaps 99%. The specificity of the test is the ability of the test to correctly identify all truly negative (non-exposed) animals. For this discussion, "true negatives" will be animals that have never been exposed to the field or vaccine virus. Reports of the use of the IDEXX ELISA test in populations of uninfected animals suggest that there are some false positive results (Camille Moore, personal communication). If in a group of 100 truly negative pigs four test positive, the specificity of the test is 96%. Thus, 96% of the time, the test will correctly identify negative animals. I do not know the exact specificity of the test. For this discussion, I have assumed that 96% is close to the actual value.
The positive predictive value is the probability that a pig is truly positive when it is test positive. Let's test three populations of 200 animals. We will assume that the prevalence of disease in these populations is 0%, 30%, and 80%.
Table 1 shows the expected test results in a PRRS-negative herd. The positive predictive value of the test is 0/8 = 0%. The negative predictive value is 192/192 = 100%. Therefore, in a naive population, we can be very confident about the negative test results, but not confident about the positive test results. The positive predictive value depends on the sensitivity and specificity of the test and the prevalence of the disease in the group of animals. As the prevalence increases, our confidence about the positive test results increases.
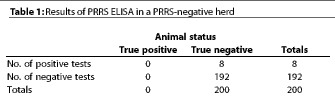
Table 2 shows the expected test results in a herd where 30% of the animals are serologically positive for PRRS (true positives). Now the positive predictive value is 59/65 = 91%, and the negative predictive value is 134/135 = 99%. This indicates that 91% of the time, a test positive animal is truly positive. At 30% prevalence, we are 91% sure about the positive test results.

Table 3 shows the expected test results in a herd where 80% of the animals are serologically positive for PRRS (true positives). In this case, the positive predictive value is 158/160 = 99%, and the negative predictive value is 38/40 = 95%. When the prevalence is high, we can be very sure about the positive test results but less confident about the negative test results. Now, only 95% of the time will a test negative animal be truly negative.

This discussion will be continued in the next issue of the Journal.
--Cate Dewey
