Original research |
Peer reviewed |
Utilizing alternative indices to compare the conformance of market hogs across three packers
John D. Roberts, DVM, PhD; John Deen, DVM, PhD; Thomas Johnson, PhD; Jay F. Levine, DVM, MPH
Cite as: Roberts JD, Deen J, Johnson T, et al. Utilizing alternative
indices to compare the conformance
of market hogs across three packers. J Swine Health
Prod. 2003;11(6):284-290. ![]() Also
available as a PDF
Also
available as a PDF
JDR, JFL: Department of Population Health and Pathobiology, College of Veterinary Medicine, North Carolina State University, Raleigh, NC 27606. JD: Department of Clinical and Population Sciences, College of Veterinary Medicine, University of Minnesota, St Paul, MN 55108. TJ: Department of Agriculture and Resource Economics, College of Agriculture and Life Sciences, North Carolina State University, Raleigh, NC 27606. Corresponding Author: Dr J.D. Roberts, NCSU-CVM, 4700 Hillsborough St, Raleigh, NC 27606; Tel: 919-513-6392; Fax: 919-513-6383; E-mail: j_roberts@ncsu.edu.
Summary
Objectives: Generalized Taguchi indices were applied to compare the carcass quality performance of a group of marketed pigs against the quality requirements of three packing companies.
Materials and methods: One hundred eighty pigs from a feeding facility were slaughtered at a packing plant. Carcass quality data was collected from the individual carcasses. Most packers determine individual carcass prices from a matrix that references carcass weight and the percent of lean meat in the carcass. Individual packers determine price using different algorithms applied to the matrices. Group carcass measurements were evaluated using three different packer matrices. The ability of the carcass group to perform for the three packers (A, B, and C) was evaluated using measures of quality performance known as sort loss, average lean premium, expected relative loss (Le), and generalized Taguchi performance (C'pm). Revenue was measured as total revenue and average carcass value.
Results: The matrix of Packer B developed the smallest Le value (0.125) and the largest C'pm index (0.947), indicating that the carcass requirements of Packer B were best satisfied. Sort loss and average lean premium could not be compared among packers. The values of revenue were comparable and Packer C attained the largest.
Discussion: Sort loss and average lean premium implied financial information concerning group conformance that was not comparable among packers. The Le provided a comparable descriptive that was easier to interpret than the C'pm.
Implications: Le and C'pm indices may provide a comparison of group carcass quality performance across different packers.
Keywords: swine, swine marketing, Taguchi indices, process capability,
process performance
Search the AASV web site for pages with similar keywords.
Received: January 9, 2003
Accepted: April 14, 2003
Approximately 97 million market hogs were sold annually to packers in the United States between 1999 and 2000.1 The hog producers received almost 10 billion US dollars annually.1 Producers were paid for market hogs on the basis of their individual carcass weights after packers penalized carcasses that exceeded the upper weight tolerance or failed to attain the lower weight tolerance. Between 1999 and 2000, producers in the United States were annually penalized an estimated $150 million for carcasses that were noncompliant with the weight tolerances of packers.2 This loss provides an incentive for producers to better understand market group weight conformance.
Producer marketing decisions are issues of timing. Producers are anxious to sell pigs, as facilities must be emptied and prepared for younger pigs.3 Simultaneously, producers postpone marketing to allow lighter weight pigs more time to gain weight.3 Producers have strategic market plans to sort market pig groups from available pigs and time the sales of those groups.3 A good marketing plan strives to fit the inherent weight variability of available pigs into a packer's pricing scheme to maximize producer profits.3-7 However, even the most profit-maximizing market hog groups contain animals that do not meet packer requirements. The conformance loss of these animals represents potential profit producers would realize if their production processes were capable of delivering pigs with less carcass variability.8 A producer may also interpret conformance loss as an incentive to sell hogs to a less restrictive packer. Producers must carefully measure and monitor market hog group carcass conformance to find potential opportunities to reduce conformance losses and increase profits.
The US swine industry currently monitors weight conformance loss with an index known as sort loss.2-5,7 The sort loss sustained by a group of carcasses is calculated as the total individual weight penalties assessed to light and heavy carcasses divided by the number of carcasses sold. Packers assess weight conformance penalties differently, so sort loss evaluations are not comparable between packers.4,5 Packers also pay premiums for carcasses that have a high percentage of lean meat. The conformance of a market group to a packer's demand for lean meat is enumerated by the term "average lean premium."4,5,7 The average lean premium paid per carcass is calculated similarly to sort loss. Terms of average lean premium also cannot be compared between packers, as premiums are awarded inconsistently.4,5 Sort loss and average lean premium relate average penalties and rewards, but neither communicates the total returns an entire market group fails to realize due to carcass nonconform-ance.8
Packers and producers could better understand carcass nonconformance loss if an alternative term were used that described the extent of total conformance loss. The alternative term would indicate the ability of a pig production process to produce pigs conforming to a packer's requirements. The alternative term would focus on the final individual carcass prices of a market group, instead of pricing segments. The alternative term would also permit valid comparisons between packers. Other industries use process performance indices (CpK, Cpm, and C'pm) to evaluate product quality performance.9-12 These indices are typically applied to industrial manufacturing processes that construct parts with a high degree of precision and accuracy, to assure the proper function of an assembled mechanism.11 Performance indices enumerate the probability that a production process, with a known variation, can create a product that will meet the conformance requirements that assure the function of the final product.9 The traditional performance index (CpK) was adapted only for gauged enumerative measurements. The CpK is not applicable to carcass pricing schemes, as it does not utilize the financial measures of penalties and premiums.11,13,14 The Taguchi indices (Cpm and C'pm) can manage financial measures.15-17 However, conventional Taguchi indices (Cpm) are not applicable to carcass quality performance, as the penalties assessed carcasses for increasing underweight are more aggressive than the penalties associated with increasing overweight.2,4,5,14 The losses associated with weight penalization must increase identically for overweight and underweight nonconformance if a Cpm index is to be used.8,12,14 A potential alternative is the generalized Taguchi performance index(C'pm), as it accommodates asymmetric loss functions.8,12,14 The C'pm can be used after a hog group is marketed to convert the financial rewards and penalties of carcass conformance into a value that describes the probability that a pig delivered with a market group performed to meet the needs of the packer. The development of a generalized Taguchi index involves a related index known as the expected relative loss (Le). The Le is of more value to producers than the C'pm, as Le evaluates the portion of possible returns that even a profit-maximizing market strategy fails to capture. A producer using a profit-maximizing marketing scheme may have a low process performance. The low performance represents an opportunity to further increase profit by changing the pig production process to produce less variable market hogs. A profit-maximizing marketer with low performance may also evaluate the performance of the same market pigs with other packers. An application of the C'pm and the Le are presented in this paper to evaluate the quality performance of a market hog group. A comparison of the quality performance values attained at three different packers was achieved by simulating the marketing of one group of hogs to all three packers on the same date.
Materials and Methods
Data collection and modeling
A North Carolina producer selected 180 hogs from a commercial swine feeding facility and shipped them to a nearby packing plant. Individual carcass weights and meat leanness were measured on every carcass during the slaughter process. Packers use a pricing matrix to price individual carcasses on the basis of their specific weight and percent of lean meat.2,4-6 Three pricing matrices that were in effect on the same date were provided by three different packers. Two of the packers, Packer A and Packer B, operated in North Carolina. Packer C was located in the Midwestern United States. All three packers measured carcass leanness with readings taken at the level of the head of the tenth rib using a Fat-O-Meater probe.18 The three pricing matrices were applied to individual carcass measurements in a spreadsheet model (Excel 97 SR-2; Microsoft Corporation, Redmond, Washington). The model produced a set of three packer prices that would have been paid for each of the 180 carcasses, simulating the marketing of the carcass group through the three packers on the same date.4 Group carcass quality performance was evaluated using indices generated from the financial outcomes. Sort losses, average lean premiums, and average carcass values were developed, as these indices are commonly used in the pork industry. Le and C'pm indices were also developed to compare group quality performance between the packers.
Developing a C'pm
The generalized Taguchi indices were developed in three steps. The first step established the relative loss of every carcass within each packer matrix. Relative loss is the portion of the financial value of an ideal carcass that a nonconforming carcass fails to achieve.8 The financial value of an ideal carcass was assumed to be the maximal price (PriceM) that would have been paid for one carcass in each application of a packer matrix.8 A maximally priced carcass would have been priced higher than other carcasses of different qualities, as its measurements were considered the closest to the packer's specified weight and leanness.8 The difference between each carcass price (PriceY) and the price of the maximally priced carcass (PriceM) was calculated. The difference was then expressed as a portion of the maximal price to derive a relative loss value (relative loss = [PriceM - PriceY] / PriceM).8 Each packer matrix produced 180 relative loss values that represented the distribution of conformance loss across the carcass group.
The next step used each group of relative loss values as a base to develop an Le value with its confidence interval. As is the case with most carcass market groups, the distribution of individual carcass relative loss values is very skewed due to the greater penalties assessed lightweight carcasses.8 A statistical technique known as "bootstrapping" was employed to provide a more accurate median estimate of relative loss from the skewed distribution. Bootstrapping used the large relative loss data set to serve as a sampling base for drawing the relative loss value for one carcass at a time, recording the valuation, and replacing the drawn relative loss value back into the data set before drawing again. Sampling with replacement was continued until a combination of 180 drawn values (n=180) was recorded. The selection of 180 relative loss values is known as a bootstrap "resample."8 Sampling with replacement was continued on the group of relative loss values until 1000 bootstrap resamples (B=1000) was established. Resampling was easily accomplished with a computer program (@RISK 4.0; Palisades Corporation, Newfield, New York). The mean of every resample was calculated and the means were sorted in ascending order. The sorted set of 1000 mean relative loss values served to "magnify" the variation of the original data set and better define the random distribution of expected variability among the carcasses. The median of all 1000 resample means was the Le of the 180 carcasses.8 A 95% confidence interval about the expected relative loss was defined by the 975th mean relative loss (the upper confidence limit), and the 25th mean relative loss (the lower confidence limit).8 A confidence of 95% assures a 2.5% risk (25 in 1000) of the random estimate being too great and a 2.5% risk of being too slight. This interval is justified, as the expressed distribution of variability was randomly drawn. Bootstrapping provides a more accurate estimate according to the central limit theorem, which states that an estimate of central tendency taken from an extremely large sample is accurate, even if the distribution is skewed.19
The last step used an algorithm to convert each Le and its confidence limits to a C'pm and its confidence limits. Le and C'pm are associated as C'pm = 1 / (3[Le]0.5).8 The exponential function is important for quality control engineering issues, as it expresses the Taguchi squared error loss function.17
The confidence intervals about the C'pm and the Le indices were used to compare modeled group performance values. The merger of two 95% confidence intervals from separate packer matrices demonstrated a lack of significant difference at a 5% level of confidence (P>.05). A separation of two 95% confidence intervals indicated that the performance values were significantly different (P<.05). The confidence intervals of Le and C'pm provided a valid method of comparing the group carcass performance modeled by the packer matrices.14
Results
The traditional indices of sort loss, average lean premium, and average carcass value were derived from the model as applied to each packer matrix. Le and C'pm indices were also developed from the model (Table 1). The Le value of Packer B was 0.125, indicating that the group achieved a level of conformance 12.5% less than an ideal market group that sustained no conformance loss. The matrix of Packer B developed the largest C'pm value and the smallest Le value (Table 1). The conformance requirements of Packer B were different from those of either Packer A or Packer C, as the 95% bootstrap confidence interval for Le and C'pm of Packer B did not infringe on those of Packer A or C (Table 2). However, the conformance requirements of Packers A and C were similar to each other, as the 95% bootstrap confidence intervals for Le and C'pm of Packers A and C overlapped (Table 2).
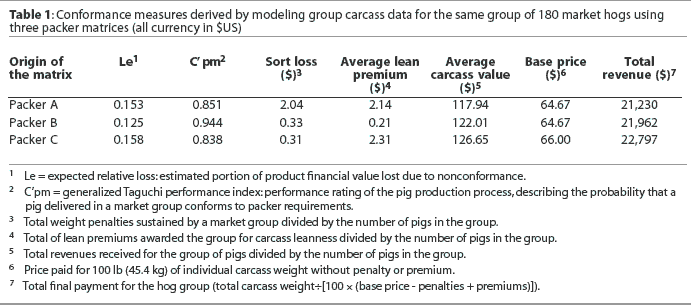

Sort loss and average lean premium per carcass developed interesting values, but were derived from dissimilar matrices and were not comparable as measures of carcass quality performance. A comparison of sort loss and average lean premium indicated that Packer A would have penalized heavily for weight nonconformance, but would have returned high lean premiums for the study hogs. Packer B would have penalized lightly for weight nonconformance and paid a comparatively smaller premium. Packer C would have penalized the producer the least for nonconforming carcass weights (Figure 1) and would have paid the largest premiums (Table 1).
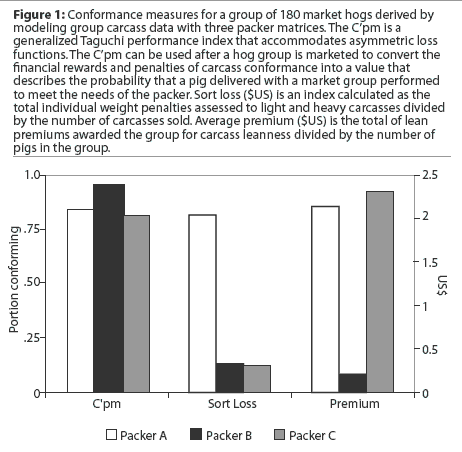
The distribution of individual carcass relative loss across the carcass group modeled with the Packer B matrix illustrated the severity of the skew of this distribution in most carcass market groups (Figure 2). The mean of the modeled individual relative losses for Packer B was 0.163 +/- 0.009 and the median was 0.146 +/- 0.009 (P =.05, Student t test). Carcass weight was inequitably dispersed about the distribution of individual carcass relative loss modeled from the Packer B matrix. The lower quartile of the carcasses with the greatest relative loss values contained all carcasses weighing less than 169 pounds. A carcass weight of 169 pounds correlates to a live weight of 220 pounds, as the average dressed carcass yield was 0.77. However, carcass leanness was evenly dispersed across the distribution. There was no significant difference in the percent of leanness assigned the carcasses in that quartile and the remaining carcasses (P =.577, Student t test).
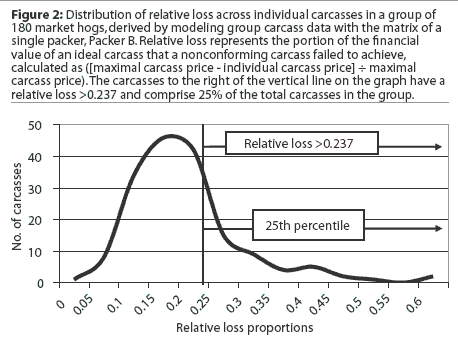
When Le and C'pm were plotted against revenue received using the Packer B group data, the association of Le and total revenue was linear, and the association of C'pm and revenue was exponential (Figure 3).
Discussion
The Le is financially comparable across packer matrices with one caveat. The readings of leanness from one packer can be modeled in the matrix of another packer only when leanness measurement methods are equivalent. Some packers use different carcass probes and some measure at different sites on the carcasses. These measurements are not equivalent. However, it is possible to adjust the carcass measurements of leanness of one packer into equitable measurements of another. The adjustment is attained accurately using a linear regression formula derived from a sample of carcasses measured using the methods of both packers.5
"Revenue" is an economic term that refers to the total income a producer receives from a packer for a market hog group. Producer profit cannot be inferred from revenue without knowledge of producer cost (revenue - cost = profit). However, the model can assume that the cost of producing the pigs represented by the carcass data was a constant value, regardless of which packer matrix was used in the model. Therefore, a positive difference in revenue between packers reflects added producer profit. In reality, there would be differences in transportation, labor, and other costs to consider when hogs are marketed to different packers.5
The modeled confidence intervals of the C'pm and Le created valid statistical comparisons of the conformance of the market group among the three packers. The largest C'pm and smallest Le were developed from the Packer B matrix, indicating that the carcass quality performance of the market group would have best satisfied Packer B. However, the largest C'pm and smallest Le did not identify the packer that would have offered the greatest total revenue for the 180 market hogs. Group quality performance and group revenue are associated, but across packers they are separate issues, conclusively addressed by different indices.8 Contrasting average carcass values between packers determined that Packer C would have paid an average of $4.64 more for each hog than Packer B. None of the group carcass conformance measures indicated the packer option that would yield the greatest group revenue. Changing production or marketing processes to increase the conformance of a market group within the same packer matrix results in increased revenue received for that or similar groups. However, changing packers to increase conformance may fail to result in increased revenue, as different packer matrices financially reward and penalize carcass conformance in different magnitudes.
Comparing the penalties of sort loss to the rewards of average lean premium indicated a lack of consistency between packers. Packer C rewarded lean carcasses to a degree that far exceeded the penalties assessed weight variability. A disparity of packer needs is expected, as some packers sell meat to certain distributors that require cuts of greater consistency. Other packers sell to many distributors that require less consistency.3 Packer C was more focused on the volume of meat commodity produced.3
The Le currently has more application within the pork industry than the C'pm.8 The modeled C'pm values described the quadratic Taguchi squared error loss function as revenue decreased exponentially in response to decreased group carcass conformance. The C'pm performs a role familiar to quality management professionals who use capability indices and six sigma loss functions.14 However, the C'pm is not financially quantitative. Many individuals who establish pig marketing strategies are concerned with managing quality to the extent that it enhances the profitability of the pig production process. The Le has better application to profitable marketing, as it quantifies financial loss due to carcass nonconformance. The extent of loss is not reflected directly, but relatively, as a portion of ideal revenue a market group did not realize. Le values express the extent of financial loss without revealing revenue or other proprietary information.
The Le is well correlated to the total revenue received for a market group, more so than the C'pm. An ideal situation would deliver all 180 carcasses with the weight and leanness of the maximally valued carcass. When group carcass quality is diminished, total revenue is decreased, and increased conformance loss results in an increased Le and a reduced C'pm, as shown in Figure 3. However, the Le and the C'pm describe decreasing revenue differently. The regression of Le and total revenue showed a perfect linear correlation, unlike the exponential association of C'pm and total revenue. Le values were reported on a 0-to-1 scale, with 0.00 at maximum total revenue and 1.00 when conformance losses expended all revenue. The C'pm values were infinitely large when total revenue was maximum. The C'pm approaches an infinitely small value as revenue decreases, but signaled a value of 0.333 when revenue was depleted. The Le communicates the extent of conformance loss better than the C'pm, as the linear 0-to-1 scale is more easily understood.
Some producers are better positioned to apply the C'pm, eg, those who market from packer-owned pig production processes. These producers approach pig production as a supply step, rather than a detached profit-maximizing process. Company customers demand a level of meat product conformance and pay for quality. Packer-owned producers are expected to deliver a level of carcass performance that assures that meat products can be fabricated to customer specifications. The C'pm defines the probability that pigs delivered by a company pig production process will meet the needs of the packing process. The probability drawn by a C'pm is more applicable to the integration of these processes than is the financial interpretation of Le.
Large producers that operate independently of packers often negotiate a profitable position in a long-term supply contract with one packer. The contract assures a continued outlet for finished pigs, which is an advantage over a strategy that independently seeks an outlet for every individual market group. Carcass quality requirements are usually part of the contract. Producers marketing through long-term contracts find value in a C'pm, since it describes the probability that their pig production process will deliver market groups of pigs that meet the tolerance limits of the contract.
An advantage of using the C'pm and Le is the robustness of carcass relative loss across various packer pricing schemes.8 An example is a pricing matrix that awards premiums and charges penalties that are proportions of the base price. Carcass relative loss (relative loss = [PriceM - PriceY] / PriceM) adapts, as any base price change that alters a relative loss numerator is balanced by a reciprocal alteration in the denominator. Changing base price does not change the relative loss values of identical carcasses if the premium and penalty proportions remain constant. Carcass relative loss also accommodates sliding-scale matrices. A sliding-scale matrix may award a maximal carcass price to several different types of carcasses in the same market group. The concept asserts that a heavier lean carcass is worth the same as a lighter carcass that is very lean. The relative loss algorithm calculates as 0 the relative loss of all maximally priced carcasses in a market group. Market groups often have more than one maximally priced carcass, but a sliding-scale matrix selects maximal carcasses of different types. This is not disruptive, as any maximally priced carcass has a relative loss of 0, regardless of weight or leanness. Relative loss is based on financial terms, not on measurements. The Le and the C'pm can function with many types of packer pricing schemes.8
A disadvantage of both the C'pm and Le is that they are difficult to calculate. Generating these indices in the field requires a computer programmed to accomplish bootstrap computations and the labor of a trained individual to administer the procedure. These factors challenge the feasibility and implementation of these indices. If valid estimates of Le and C'pm were possible without bootstrapping, the computations would be simple. The number of pigs in most market groups is quite large, and it is intuitive to assume that the determination of Le gains little accuracy from bootstrapping. This is not the case. Even large market groups have severely asymmetric carcass relative loss distributions. The distribution of individual relative loss as priced by the Packer B matrix illustrates the severity of the asymmetric skew. The mean and median of individual relative loss was compared to the Le derived from bootstrapping. The abbreviated estimation of mean and median relative loss failed to manage the skewed data as effectively as bootstrapping. The average relative loss estimate was more than 30% greater than the Le. The median estimate was more than 16% greater than the Le. Neither the 95% confidence interval about the average relative loss estimate nor the median relative loss estimate entered the 95% bootstrap confidence interval of the Le. This indicates that the simplified estimates are so different that they were not within a 5% random probability of the bootstrap estimate (Le). Bootstrapping appears to be critical to the accurate estimation of the Le.
Carcass leanness was evenly dispersed about the distribution of carcass relative loss modeled from the Packer B matrix. This finding suggests that measures of group Le would mostly likely increase due to decreased leanness across an entire market group. However, carcass weight was dispersed inequitably. If an abrupt increase were noted in expected relative loss monitors, it would be more likely that increased numbers of lightweight pigs were being included in market groups. It would be less likely that all marketed carcasses were suddenly less lean.
A packer pricing matrix incorporates two components to price market hogs: base pricing and relative pricing.4,8,14 The base price offers a price per pound of carcass. Base pricing changes frequently to adjust for a fluctuating market hog supply and packer demand.8 The relative price is derived from the supplemental penalties and premiums assigned for carcass quality. Packers rarely reassign the tolerance limits related to carcass weight and carcass leanness, so relative pricing changes infrequently.8 The C'pm and Le have an advantage, as they are sensitive only to the relative pricing component, even though base pricing is included in their derivation.8,14 The lack of sensitivity to base pricing results from the computation of carcass relative loss (relative loss = [PriceM- PriceY] / PriceM). The base price is a constant for a market group that cancels across the numerator and the denominator. Sort loss and average lean premium are also insensitive to base pricing, as base pricing is not included in the derivation of either.
The packer pricing matrix often gives lean premiums on one hand and charges weight penalties on the other.5 The concept is illustrated by Packer B, who imparts a sort loss smaller than either Packer A or C, but also awards a negligible average lean premium. A market evaluation of sort loss must consider the concurrent average lean premium to entirely account the impact on revenue. The duality of sort loss and average lean premium is a confusing disadvantage. Some producers subtract sort loss from average lean premium and express net premium to reduce the confusion. Net premium is more easily understood, but does not reference an ideal group market. Le evaluates the combined financial impact of group carcass weight conformance and carcass leanness with one index. Le also references the ideal market group, allowing description of the entire amount of revenue the group failed to achieve.
Le will signal higher values when market group carcass performance adversely affects group carcass revenues. The signal suggests that the producer must act to affect carcass weight conformance, carcass leanness, or both. Carcass leanness is primarily determined by factors that are implemented and expressed in the long term. Changing the genetic background of finishing pigs is an example. It may easily take 2 years to influence the genetics of 40% of each finishing pig group in a large production system. It is difficult for producers to immediately improve Le by intervening to increase carcass leanness. However, producers can immediately change market hog selection strategy to deliver market groups with more consistent live weights, if the strategy is not profit maximized. Live weight distributions of market hog groups are highly correlated with group carcass weight distributions.4 However, the amount of live weight variability that can be reduced is limited, as space to retain pigs is scarce and further division of market groups increases transportation and labor costs.4 Producers may resort to other options that change the production process to produce groups of more uniform pigs. Some retain lightweight pigs and continue to grow them in specialized facilities. Other producers may change the marketing process. A few producers divide highly variable market groups, sending compliant pigs to a packer that rewards consistency and the remaining lightweight pigs to another packer that tolerates lighter carcasses. The producers that best understand the carcass performance of their pigs, their production process, and their marketing options are better prepared to increase profits through innovative plans.
The model has shown that the utility of sort loss and average lean premium are limited in comparison to the Le. The substitution of Le for sort loss and average lean premium may not yet be feasible. However, the model indicates that the industry's use of sort loss and average lean premium as carcass conformance indices often obscures adequate understanding of the relationship of group carcass performance and revenue. If the Le is not a viable alternative, the alternative should have the features of the Le.
Implications
- Several performance indices are used by other industries to measure the ability of manufacturing processes to meet the quality requirements of customers.
- The C'pm and the Le indices each provided a valid measure of the carcass quality performance of a group of market hog carcasses.
- The C'pm and Le indices described the ability of the marketed carcass group to meet matrix requirements, provided valid comparisons across three packer matrices, and expressed the entire revenue lost to carcass nonconformance.
- Average lean premium and sort loss did not describe the ability of the marketed carcass group to meet matrix requirements, were not comparable across different packer matrices, and did not express the entire revenue lost to carcass nonconformance.
Acknowledgement
The State of North Carolina through the College of Veterinary Medicine Research Fund provided the funding for this study.
References - refereed
3. Roberts JD. Minimizing market weight variation in swine through strategic sorting [PhD thesis]. Raleigh, North Carolina: North Carolina State University; 1998:58-80.
9. Quesenberry CP. SPC Methods for Quality Improvement. 1st ed. New York, New York: John Wiley and Sons; 1997:466-485.
10. Kane VE. Defect Prevention. 1st ed. New York, New York: Marcel Dekker; 1989:266-287.
11. Evans JR, Lindsay WM. The Management and Control of Quality. 2nd ed. New York, New York: West Publishing Company; 1993:48-53.
12. Balamurali K. Construction of a generalized robust Taguchi capability index. J Appl Stat. 2002;29:967-971.
13. Ganeshan R, Kulkarni S, Boone T. Production economics and process quality: A Taguchi perspective. Int J Prod Econ. 2001;71:343-350.
14. Johnson T. The relationship of Cpm to squared error loss. J Quality Tech. 1992;24:211-215.
16. Snow JM. Rating quality and selecting suppliers using Taguchi loss functions. Naval Eng J. 1993;105:51-58.
17. Sauers DG. Using the Taguchi loss function to reduce common-cause variation. Qual Eng. 2000;12:245-253.
19. Remington RD, Schork MA. Statistics with Application to the Biomedical and Health Sciences. 2nd ed. Englewood Cliffs, New Jersey: Prentice-Hall; 1985:116-118.
References - non refereed
1. United States Department of Agriculture - National Agricultural Statistics Service. Statistical Highlights of US Agricultural: 2001 and 2002. Washington, DC: NASS. 2002;11:8-16.
2. Dritz S. Sort loss influence on carcass merit premiums. Swine Update. 1992;3:1-3.
4. Lawrence B. Are you selling your pigs short? Swine Solutions. 2002;1:1-3.
5. McMahon K. Untangling the maze of packer prices. Nat Hog Farm. 1994;15:50-52.
6. Smith R. Database comparisons can turn information into knowledge. Feedstuffs. 1994;66(35):31.
7. Estienne M. A weighty problem. Delmarva Farm. 1992;10:17.
8. Johnson T. Capability measures for general loss functions. Proc Am Soc Agric Eng. Atlanta, Georgia. June 1992. Paper 926004.
15. Tunner J. Is an out-of-spec product really out of spec? The Taguchi loss function can estimate the dollar value of reduced variability. Qual Progress. 1990;23:57-59.
18. Government of Ireland, Office of the Attorney General. Pig carcase (grading) regulations. Irish Statute Book Database, Statutory Instruments. 1988; 365:1.
